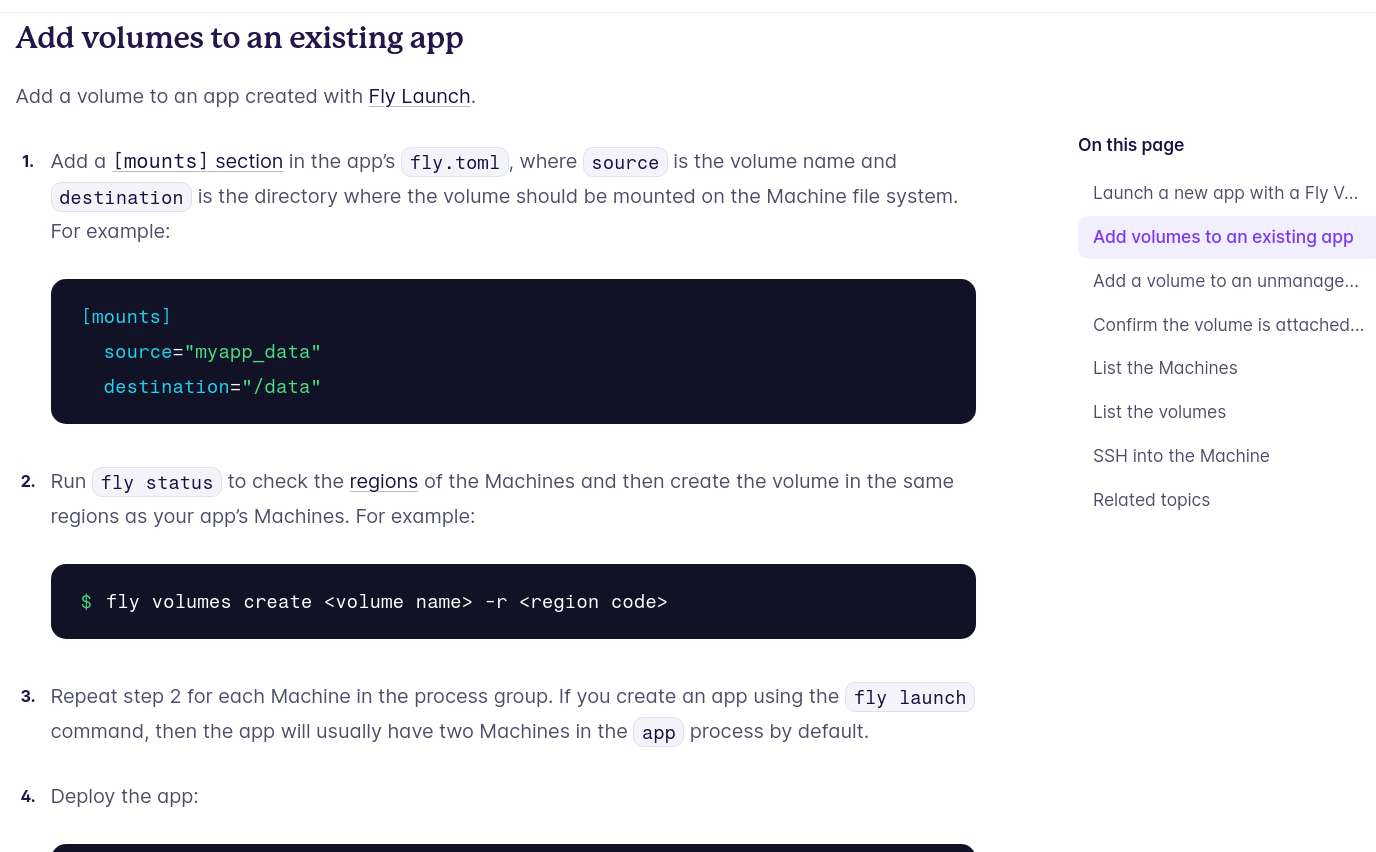
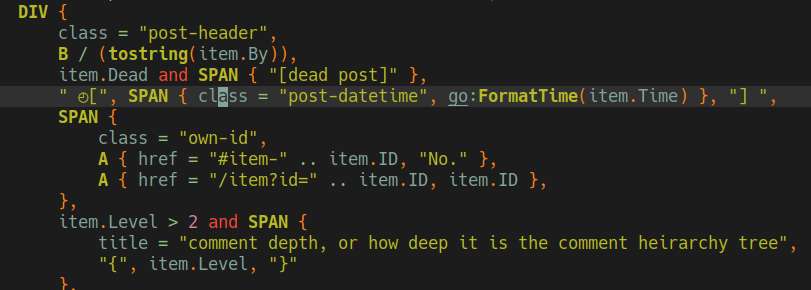
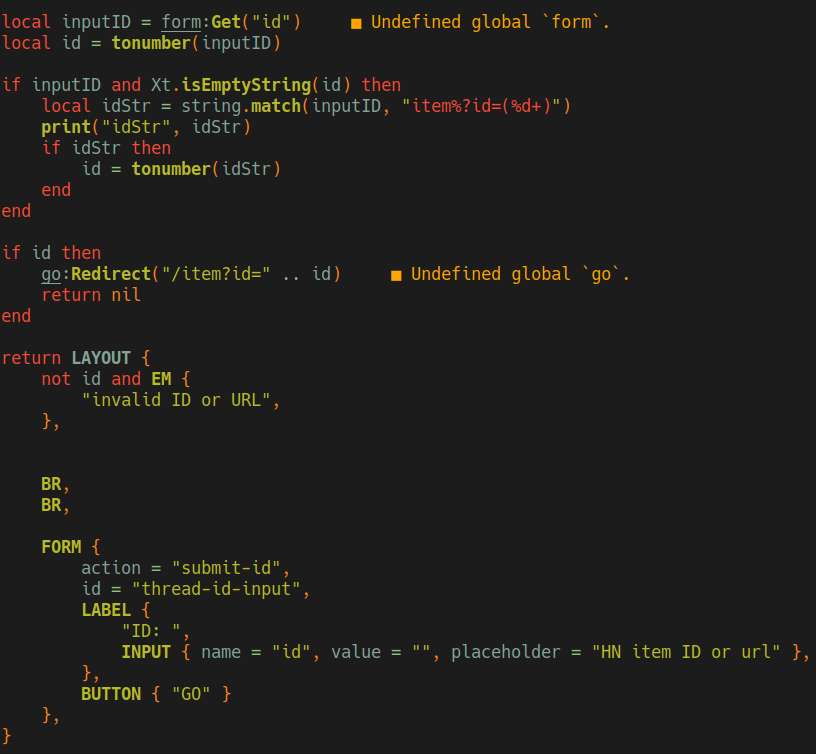
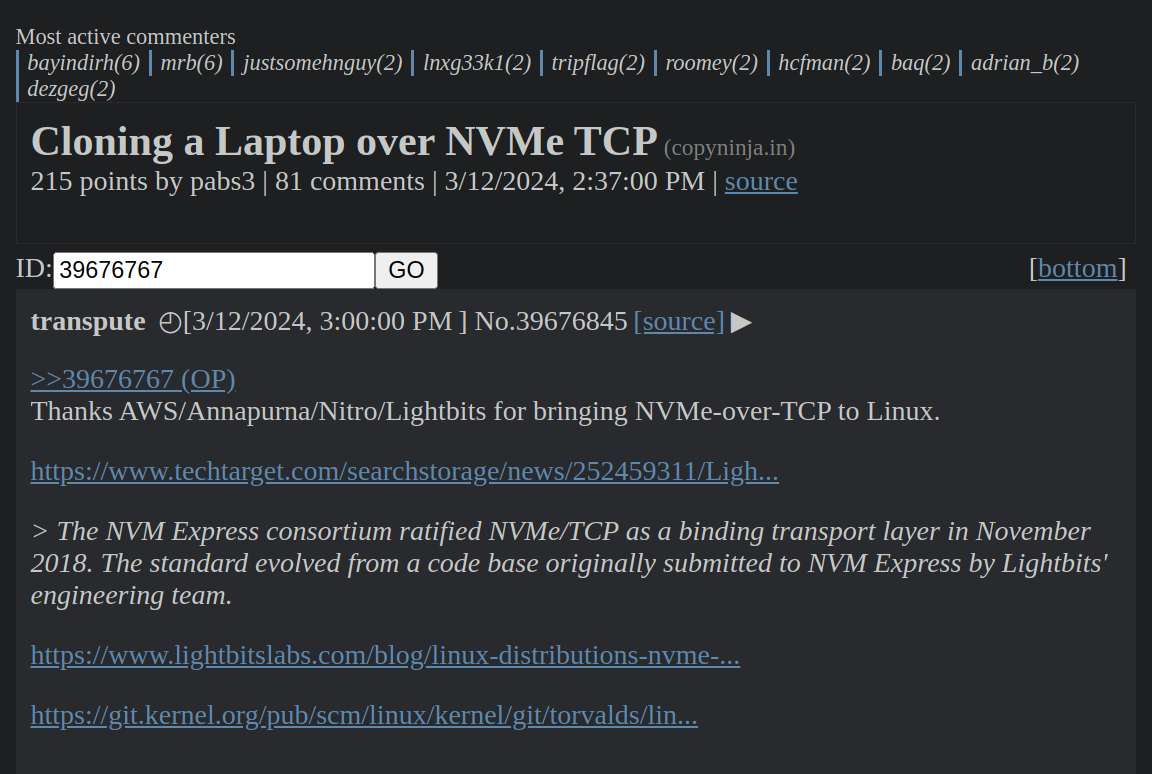
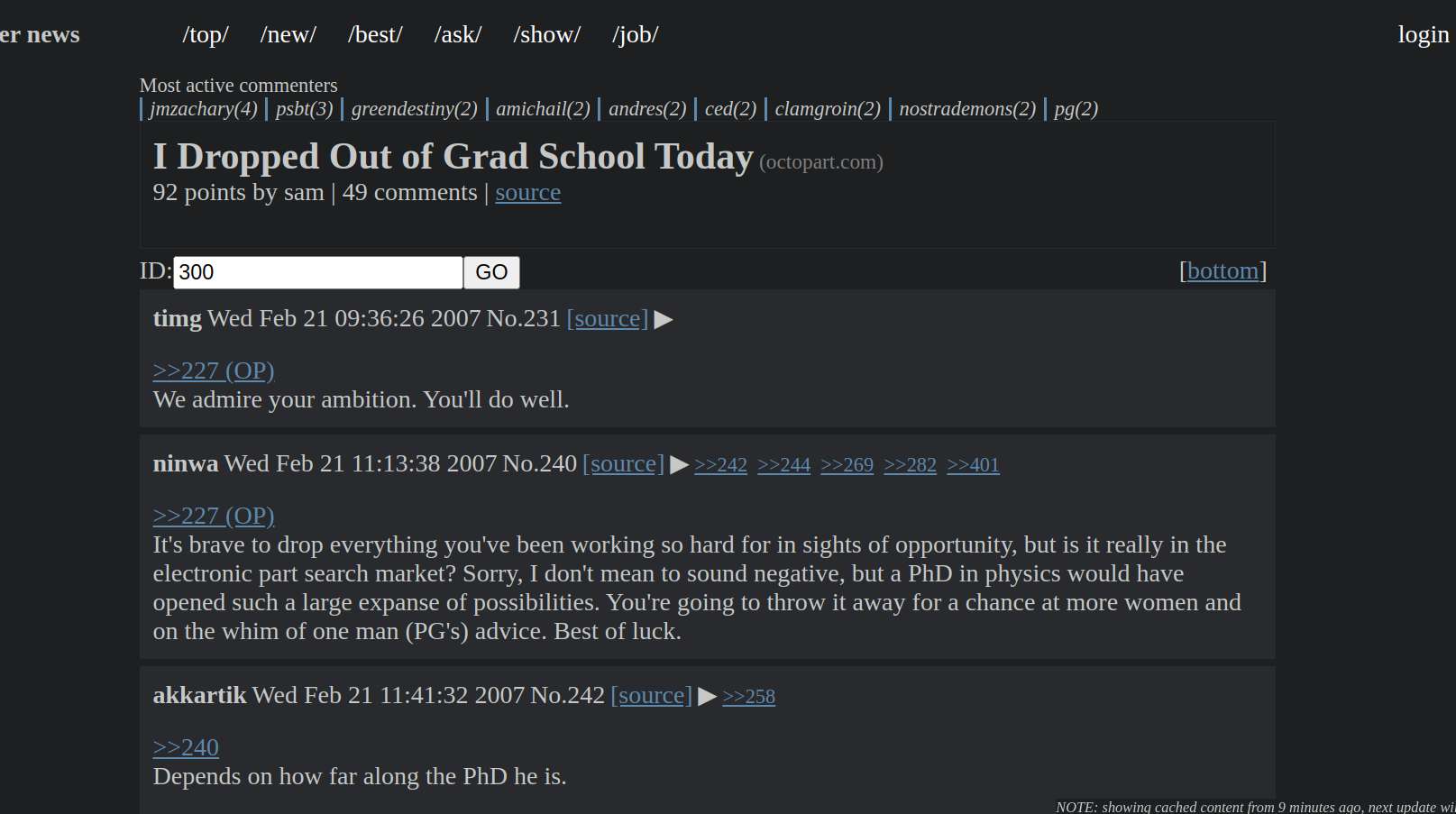
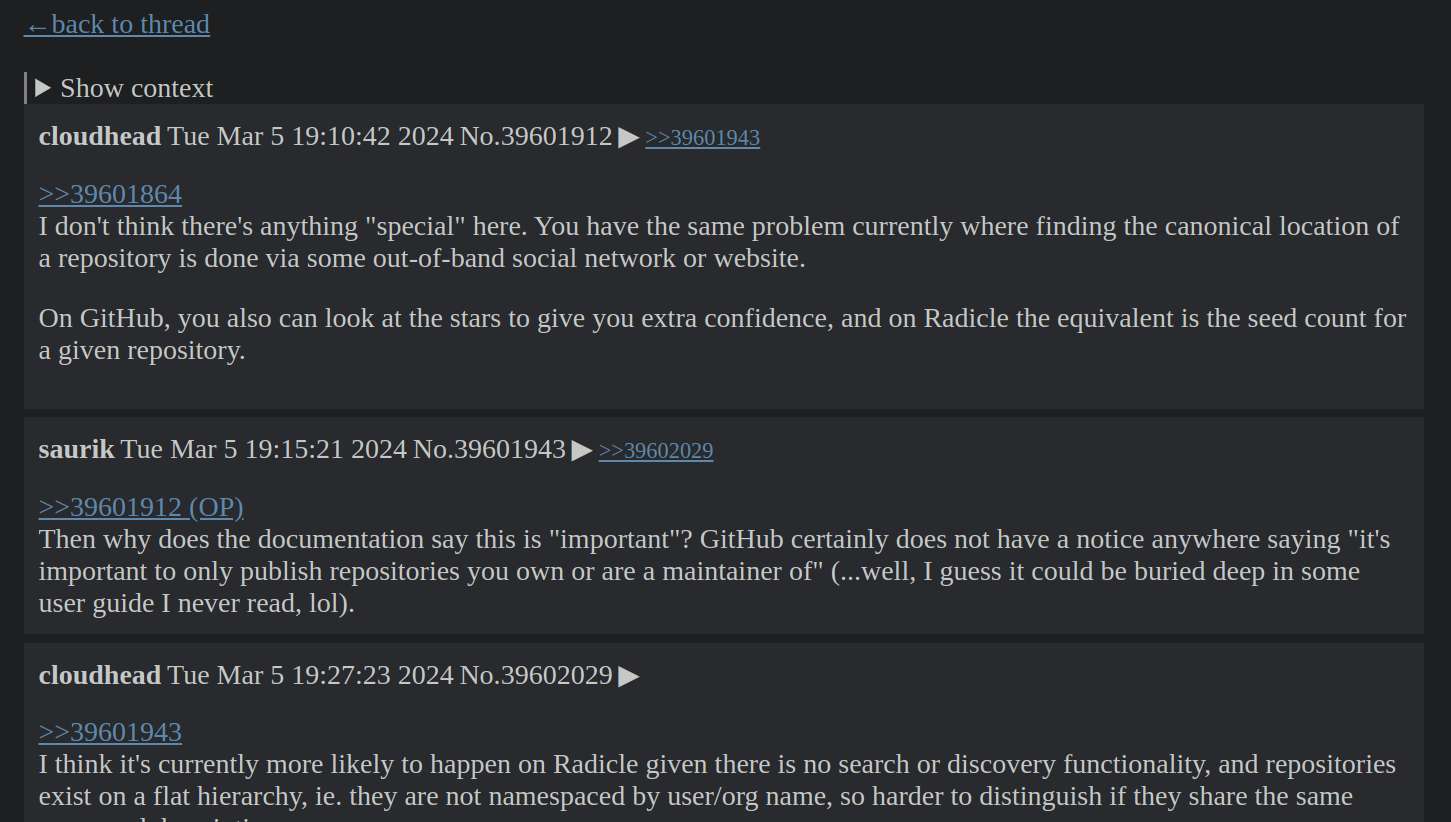
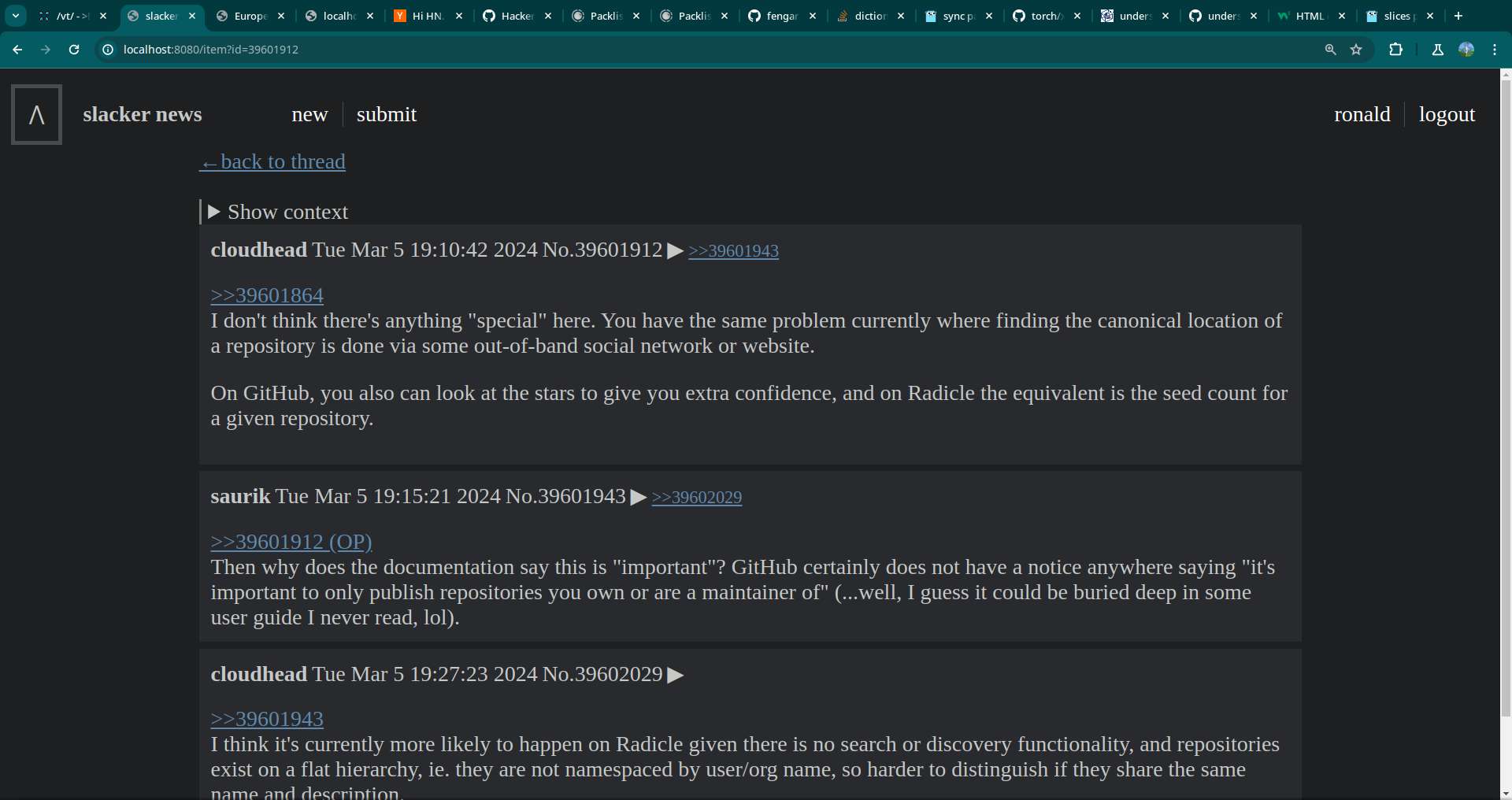
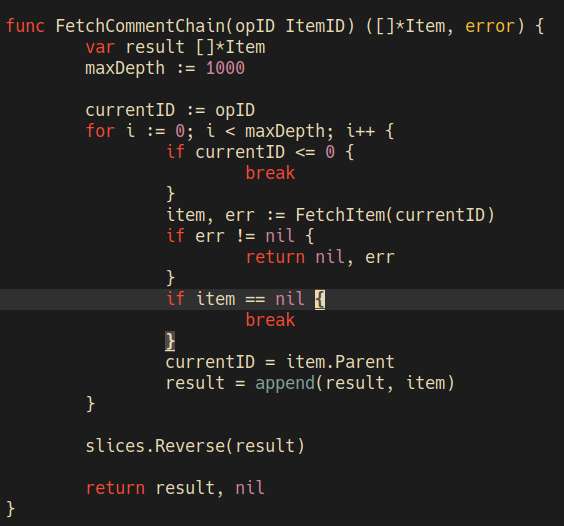
Worked on SN, I fixed the datetime so that it server-renders the date with UTC format, then converts that to localtime on the client side. I also added some textbox to easily view HN URLs.
I also looked at the fly logs why my cached json arent' working, it seems that they get deleted before the scheduled time. The logs says it periodically shutdowns the machine when the server is inactive. The fix is to use actual fly.io volumes for persistent storage.
And my quest to devise my own manual long division continues. I tried dividing and factoring several numbers numbers in my notebook, some small and some large-ish. Several observations:
- if I can't get rid of the ~, then it's (likely) not evenly divisible
- I can express larger numbers as a sum of exponential 10s such as: 123 = 1*10^2 + 2*10^1 + 3*10^0
- I should avoid distributing ~ over the sum, since it becomes even harder to solve
- Sometimes I have to add terms together to make them factorable
-
I can further factor these base exponentials to help see some factors:
So here, I could see at a glance that 735 is evenly divisible by 5, without doing full division or factoring.735 = 7*10^2 + 3*10^1 + 5 = 7*5*2*5*2 + 3*5*2 + 5 = 5(7*2*5*2 + 3*2 + 1) - Going further, I could try converting base10 to another baseN to help see the factors at a glance (in theory, I haven't tried)
With that, my division method would then be first to factor out the divisor and the dividend (prime factorization it's called it seems), then cancel out any inverses. To some extent, it works. I managed to do division even for larger numbers like 12345.
Sadly, this doesn't necessarily mean that if I don't see any obvious factors then it's a prime number. Naively I thought that was the case, I quickly ran into counterexamples, most damning of which is the quadruply nice number 469, which is a product of two prime numbers 7 and 67!?! My supposed method broke down, all is lost, god is dead and/or mad, what am I even doing with my life again.
Just kidding (maybe). I'm just missing some important detail.
469
= (2^4)(5^2) + (2^2)(3)(5) + 3(3)
469
= 6(7)Then a thought occured to me: what are real numbers? Do they even exist? Aren't they just an artifact of decimal notation? Of course, some math teacher would bonk me in the head, and point to irrational numbers. But no, what if I want to reject the concept of real numbers, out of uncalled spite, and that irrational numbers can be perfectly expressed as a ratio of two numbers, with some slight tweak in the notation and the base axioms. Maybe these dumb irrationals belong on a separate number line.
Okay, if I'm asking these crazy questions, it's time to take a break. I'll probably answer and disprove my own questions sooner or later as I go along.
To continue from yesterday, to find a way to do factoring and division, I have to ask, what does division mean anyway? What does evenly divisible mean? What's remainder? With some faint recollection of some wikipedia article, after some scribbling, I manage to come up with:
x = ab + cMoving stuffs around:
x = ab + c (1)
x - ab = c (2)
xa~ = b + ca~ (3)
xa~ = b
65 = 2*x + c
Let x = 31
65 = 2*31 + c
65 = 62 + c
65 - 62 = c
c = 3What about if I let Let x = 32
65 = 2*32 + c
65 = 64 + c
c = 1What does this all mean for me? What does a negative remainder mean, and why don't I see it in the wild? Setting that aside for now, from here it's clear that 65 cannot be evenly be divided by 2 (where c = 0). But if I want to divide by 2 anyway, I get 32 with a remainder of 1.
Checking it in python:
>>> 65/2
32.5
xa~ = b + ca~ (3)
65*2~ = 32 + 1*2~
= 32 + 0.5
= 32.5
32.5 = 32 + 5*10~
= 32 + 1*2~Then again, I still don't have a methodical approach of doing long division besides doing trial and error. On the other hand, I could now do fizzbuzz without using the modulo operator. Well, actually I already did that before using a weird alien assembly language , but still.
So today is 11th of March, which means march is practically half-way over, and if I let myself carelessly blink a few more times, it'd be April before I knew it. Time sure is bananas when it comes to flying so fast. I feel like listening again to the song "Heaven" from the game Persona.
What have I been even doing this this March? I said I was going to review my logs this weekend, but I didn't feel like it, too lazy. Most notable I did for the weekend was trying to defeat the final-final boss on Ys, I always die at the last 1000 HP of the boss. I regret going for the hard difficulty, now I can't move on to the other games, and it's a bit stressful trying to push through. I feel I didn't even get to relax this weekend.
As for today, I didn't do much, I've been scribbling away on my notebook like a madman, fixated on finding a way to do long division using my own method of multiplicative inverses. I wasn't toiling on my own volition, I was actually enjoying doing bad arithmetic, I'd make the simplest mistakes that would make a gradeschool teacher laugh. Maybe there's some dopamine hit when I rediscover some trivial mathematical properties on my own. I think to myself, huh so that's why, I can't believe I went through my adult life without knowing this basic fact.
School taught me surface level knowledge how to do arithmetic by mechanically applying algorithms. Or maybe they did teach the underlying insights, just that I wasn't paying attention. I was actually a very distracted student, the world around me would just blur during classroom hours, my mind would wander to a distant fantasy land. To my surprise, I still managed to pass with an average grade on my highschool days. College is different though.
Anyways, back on topic, what I was trying to do was to be able to do "long division" using just multiplicative inverses. So the idea would be:
12345 / 45
= (12345)45~
= (12345)9~5~
(4)(12)(3)(6)4~5~
= (4)(4~)(12)(3)(6)(5~) reorder
= (1)(12)(3)(6)(5~) substitute, 4*4~ = 1
= (12)(3)(6)(5~) remove 1, since 1*x = x
= (12345)45~
= (123(4)(5)45~
= (123(4)(5)4~5~
= (123(4)(5)9~5~
= (123(4)9~There has to be a better way. Applying division with inverses would be very easy if I could just have the form (x1)(x2)(x2)... As it turns out, that's called factoring, so my task shifted to searching how to do factoring by hand. But to do factoring, I have to do division, so what then? I found myself asking a question similar to wondering if a chicken or egg came first. There is another way, which is by trial and error, guessing if a number evenly divides another number.
Well, this log has gotten a bit too long, I'll continue this later. Time for a walk before supper.
Well, for some reason, now I'm trying to come up with my own division algorithm using only addition and multiplication. Partially, because I actually forgot how to do division by hand on paper, but also because of my curiosity to discover things for myself from first principles. Nothing new with what I'm doing, I'm sure someone already thought of these things around a thousand years ago.
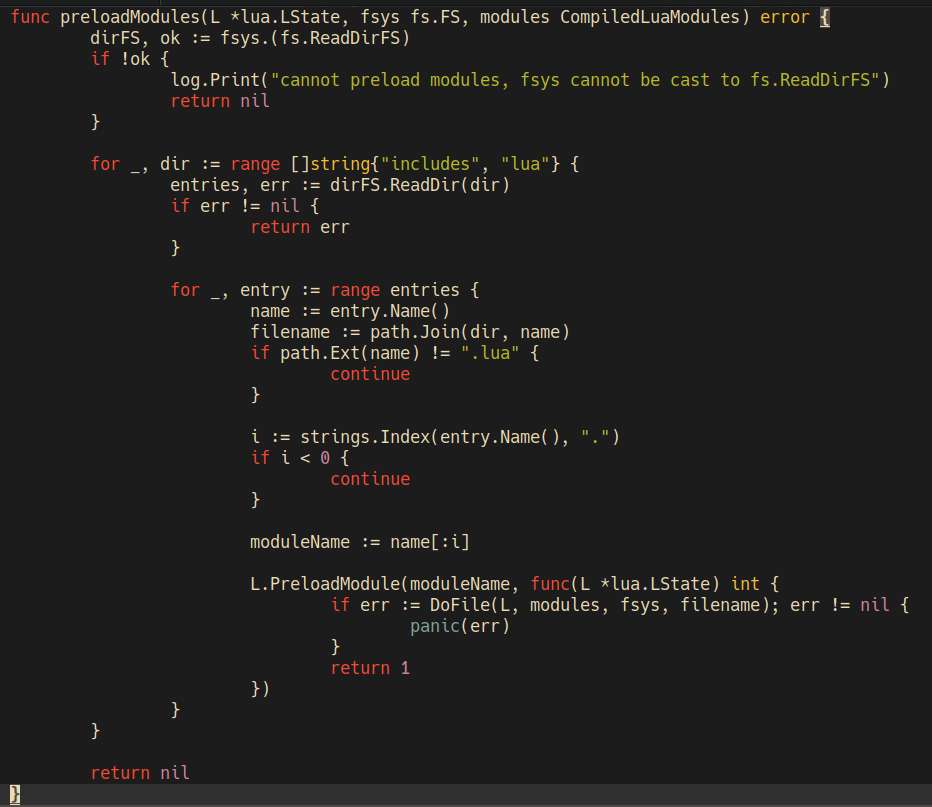
I did some changes so that the lua code is compiled and preloaded. Supposedly this should reduce memory usage. And I think the average request time went down too, sort of.
Aha, I managed to deploy slacker news on fly.io surprisingly without much problem, now I can use it on my phone too. I have unused 500 fly.io credits that I got as a bonus for applying for a job at fly.io. Unfortunately, I got rejected, but at least I got free credits in return.
I wonder how long those $500 credit will last with my shitty app though. More importantly, I hope it doesn't get ddos'ed and put me in a massive debt? I recently read something like that, I can't remember the HN thread specifically.
I left an opened pack of pocky sticks in my desk and when I came back just now my desk was filled with tiny itchy-bitey ants. I poured vineger and wiped them away, but they still managed to bite my hands, now it's all itchy. Well, nothing remarkable.
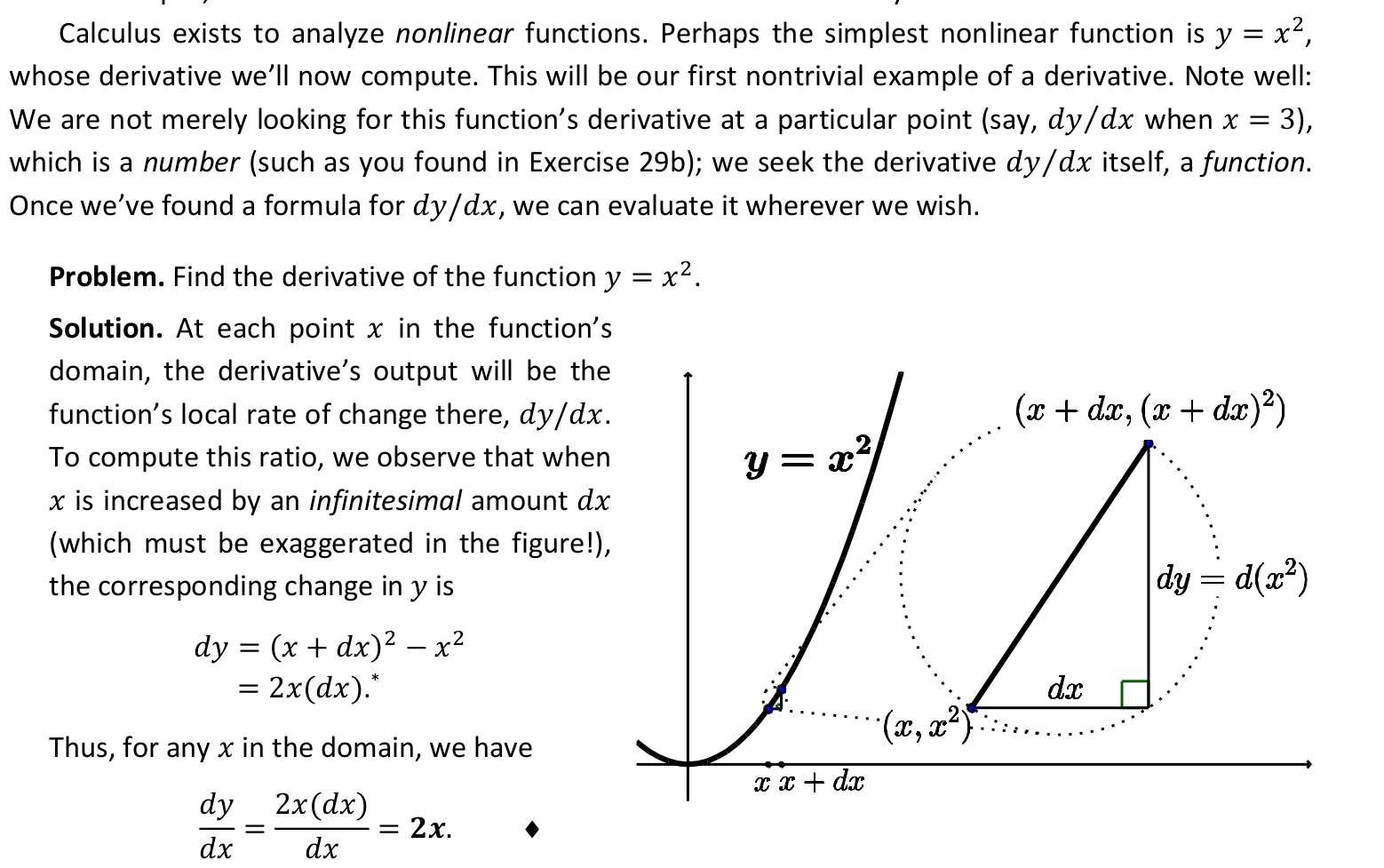
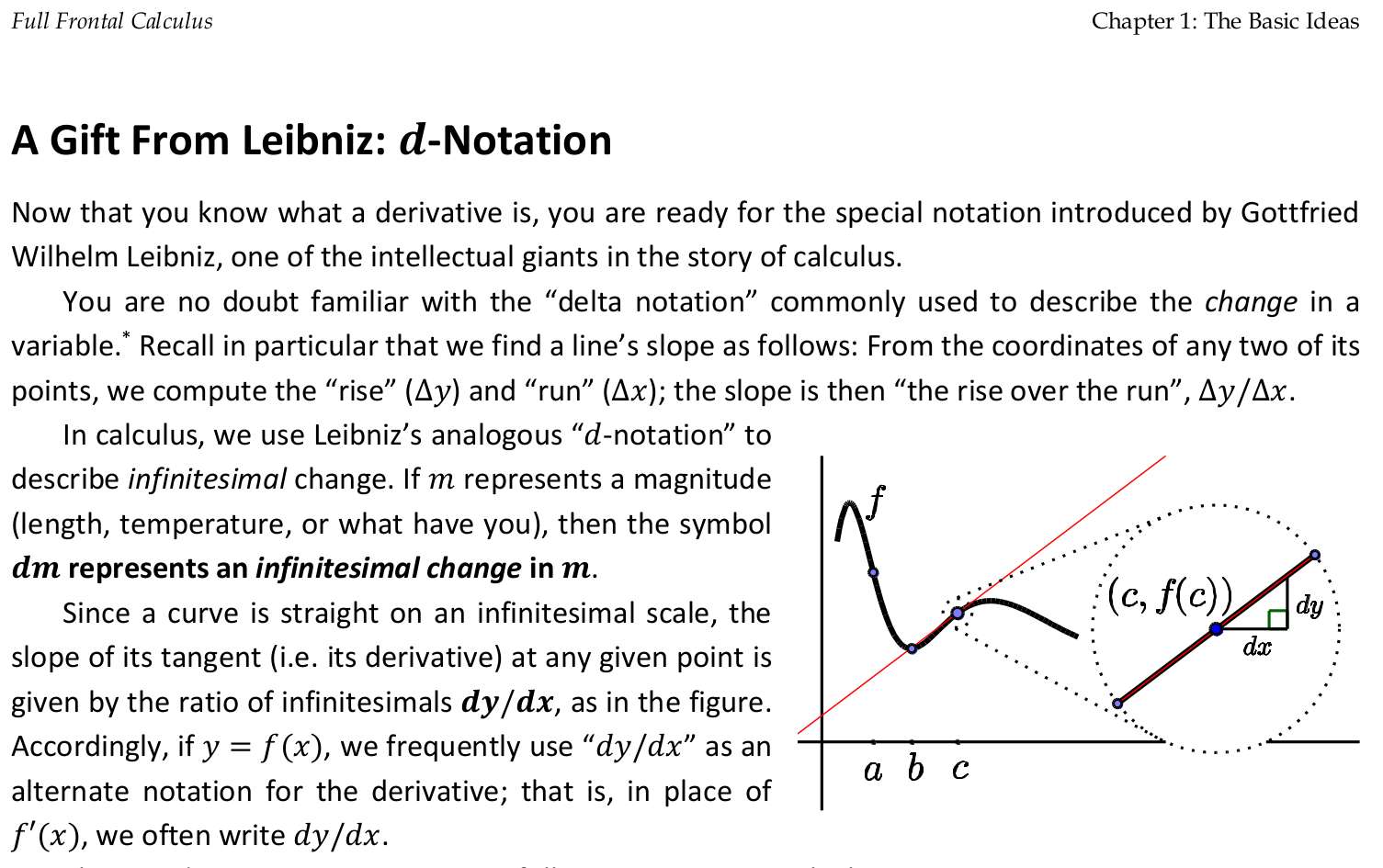
Continued reading FFC, or tried to read. On page 20, I see some very inadequate explanation for finding the derivative for x², at least compared to Keisler's explanation. It's probably more simpler, but now I have more question than answers if this was my first calculus book.
Well, to be fair, I'm not even reading intently that much, but at this point, I'm just looking for something to complain about. I'd be better off reviewing the earlier chapters of Keisler's book again.
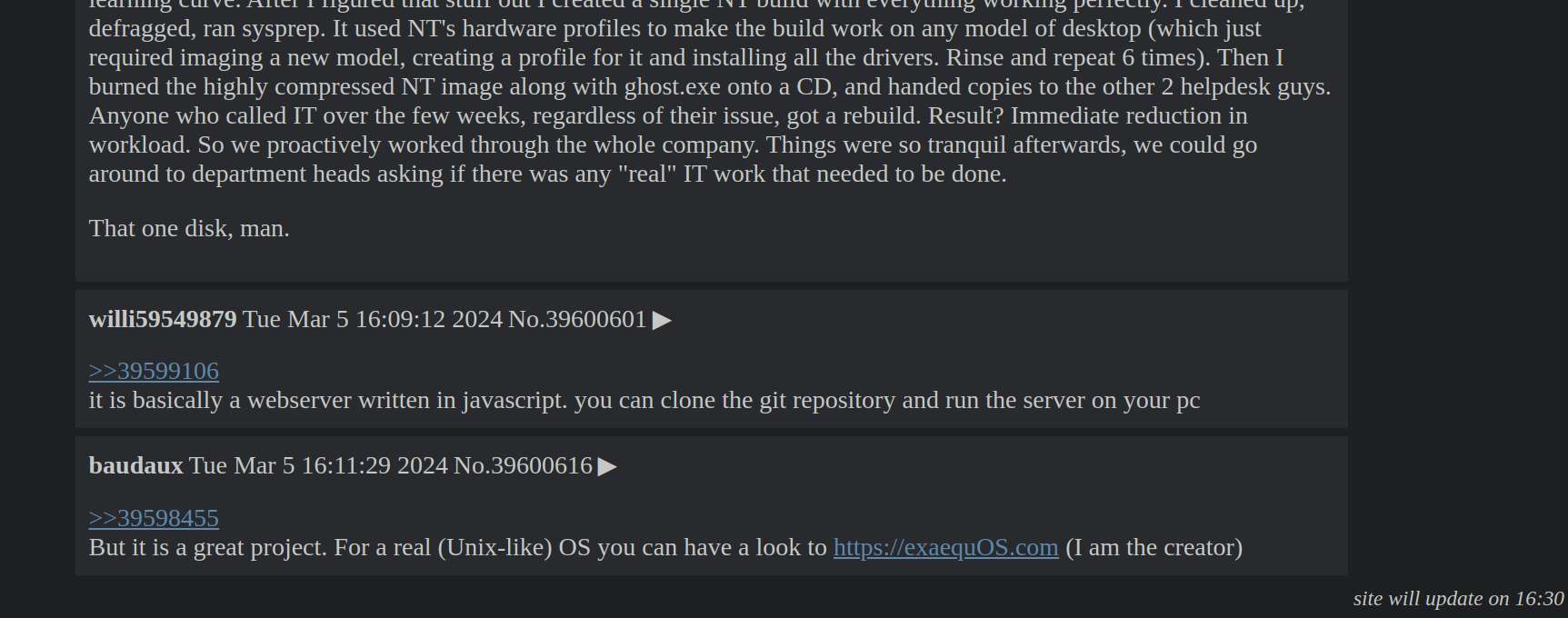
Looking at my logs, it has been 14 days now since I started working on SN Err, the lua markdown library I'm using can't handle anchor # inside a link. Oh well.
Look back further, it has been more than a month now since I started logging my daily activites. I think I'll review it this weekend to get an idea what I need to change or improve on. I wasn't actually consistent with logging what I did for a day. What was logged was mostly my time on the computer, and not much else outside that. Well, there's not much else to say when it comes to my daily routine. I live in a tiny hikikomori NEET world.
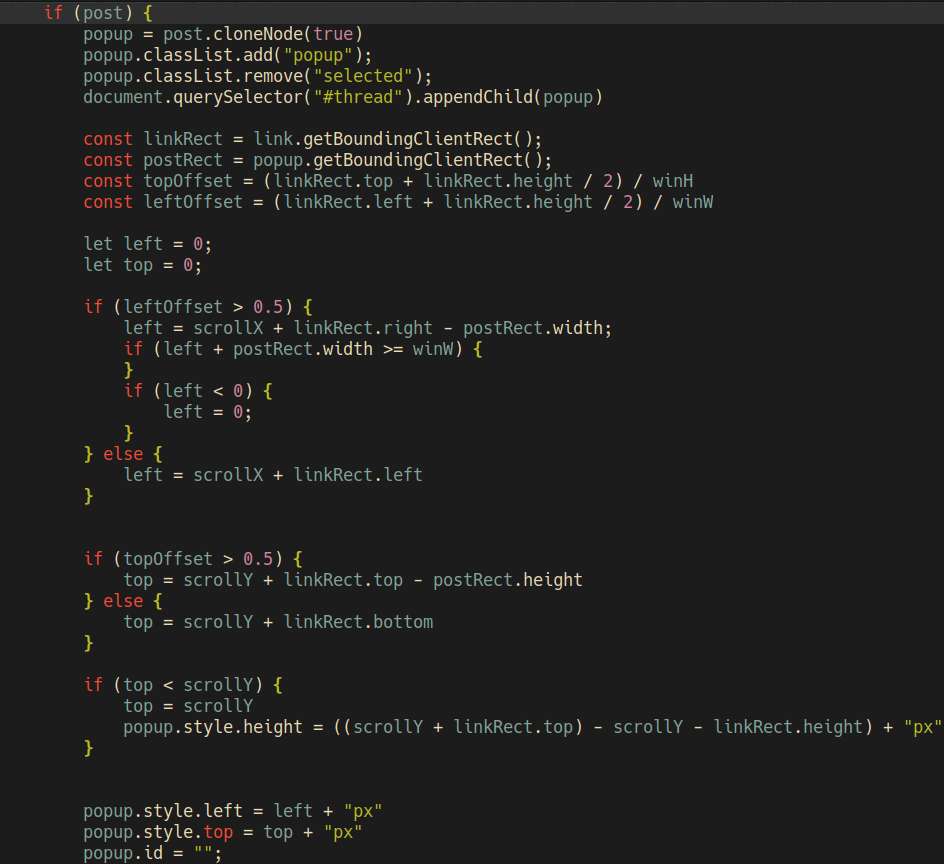
Worked on SN, fixed some filesystem errors when creating a release build. There's definitely a bunch of added complexity by having a self-contained binary with the assets embedded, not sure if this is worth it. For now, I managed to make it work, I fixed the errors by replacing direct calls to os.Stat with my own fsStat(fs, filename).
I'm more or less almost done with the project, it's quite usable with its current state. I will be using this to read HN from now on.
My original goal was to create an HN clone to test my lua templating library. But creating an HN frontend works as well. I'm convinced using lua as an alternative templating engine works quite well, I might actually use it for more web projects in the future.
I'm still considering whether I should still try creating a full HN clone. It's not actually easy running a forum. For one, I don't have the (financial) resources to maintain it. Second, no one will use it but me. Third, it might get defaced or hacked quite easily. Despite all that, I feel like just doing it anyway. Try reduce server load, I could aggresively just cache everything, and just update the site for one or two times a day. Or not.
For now, I think I'll continue watching that video titled "Godot 4 - Tiled Dungeon Environment From Scratch".
Read a bit of Full Frontal Calculus (FFC), I mostly read and didn't do the exercises. I would have probably been already lost by page 15, but good thing I already have a good intuition of what this all means, so it's easier to follow. Basically, a recap.
Played around with my rocketbook again. I tried answering my own question, how do I express multiplication and division with addition and subtraction.
Multiplication of two numbers x and y is just
xy = x + x + x ... + x
^ y times
xy = y + y + y ... + y
^ x times
x + y = xy(x~ + y~)
xy = (x + y)(x~ + y~)~
xy = (x + y) / (x~ + y~)The sum of inverses sure do come up a lot, maybe there is another way of expressing it? What about
1 = 2~ + 2~
1 = 3~ + 3~ + 3~
1 = 4~ + 4~ + 4~ + 4~
1 = 5~ + 5~ + 5~ + 5~ + 5~
x + y = xy(x~ + y~)
xy(x~ + y~) = x + y
x~ + y~ = (x + y)x~y~
2~ + 2~ = (2 + 2)(2*2)~
2~ + 2~ = 4(4)~
3~ + 3~ + 3~
= (3+3)(3~)(3~) + 3~
= (3+3)[(3)(3)]~ + 3~
= [(3+3)~(3)(3)]~ + 3~
= (_ + 3)[(_)*3]~
= ([(3+3)~(3)(3)] + 3)[[(3+3)~(3)(3)]*3]~What about expressing division in terms of addition or subtraction?
12 / 4
= 12 + -3 + -3 + -3
= 12 + -(3 + 3 + 3 + 3) + 3
= 12 + 3*4 - 3
12(4~) = 3
12(4~) = 3I did plenty of stuffs today with SN, I added showing the comment chain (post context) and top frequent participants in a thread. I also added some cache clearing every 30 minutes, that way, I will only be forced to revisit a thread after half an hour, instead of compulsively checking and rechecking a thread every other minute.
The messiest code is the UI lua/html code, which isn't really unexpected. On the positive side, it's quite easy to modify or add new changes. And it still performs relatively well, less or around 100ms per 100 comments. Sure, text/template might be way, way faster, but it's not as flexible, or even quite painful to use.
The external http request are still by far the slowest though, the filesystem caching is required.
To fill my gaps in my intuition and understanding, I started reading another book called "Full frontal calculus" by Seth Braver. It's surprisingly amusing to read, particularly the writing style of the author, where he uses religiuous analogies to describe the divide between limit-based calculus and infinitesimal calculus. It's certainly a refreshing way of explaining as opposed to the a bit overly dry prose from the other calculus book I was reading. I don't suppose to say that this is better pedagogically speaking, but it's certainly more entertaining.
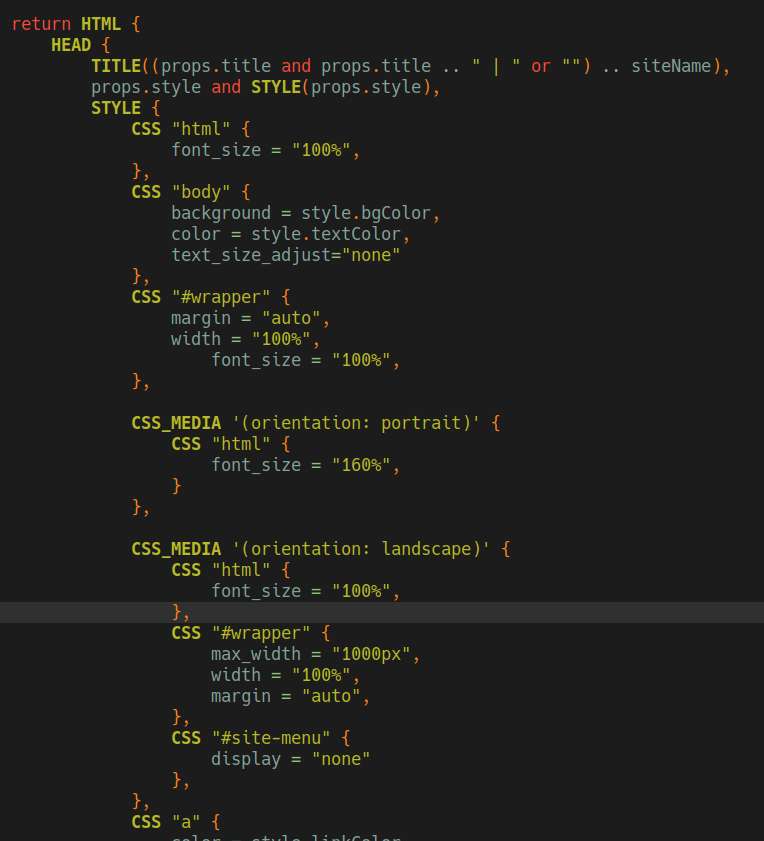
Well, some way or the other, I managed to make the SN mobile friendly-ish, it's now useable at least. The auto-adjusting font-size is pretty maddening though when on mobile. The rem unit is supposed to make the font-size relative to the root font-size, so why is some texts are still changing and appears smaller than the rest?
As it turns out, there's an exception and I have to explicitly set `text-size-adjust: none` to disable this behaviour. Some say this isn't a CSS best practice, but screw that.
This early afternoon, I also made some changes in the backend, fixed and simplified some problematic code that's causing race conditions. I also added an option to cache loaded lua modules, to speed things a little.
Played around with the notebook, I could more or less get apply the division rule with power rule and product rule. Or really, I only ever need sum rule and product rule. But I can see why there are separate rules for each, since it's not always trivial or obvious, even a bit tedious, to get the directive directly from just the sum and product rule.
But, I'm still not comfortable with the syntax. When it says differential of a dependent variable, it's talking about differential of a function, right? Then, it goes around adding functions together, which is essentially a type error. Likely, it's implied and goes without saying that it's the result of the function that's being added together, not the function themselves.
Nope, my entire being rejects this convention. Where's the fully typed math syntax, I want it.